Executive transport aircraft with truss-braced wing (World's First)

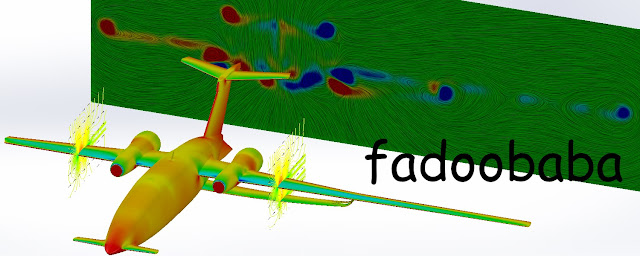
     To explore large-er aspect ratio wings; one fine morning, I just thought it would be fun to put a truss-braced wing in a Piaggio P.180 "Avanti". The modified design CAD files are is available here. A comparison is shown in Fig. 1. I am too lazy to make 2 separate airplanes so I modified half of it so I can run a CFD analysis using one model and one mesh 🤣. A slight modification about which I will write later is the positioning of the flaps and ailerons. These are moved to the truss part from the main wing in the original design. The aspect ratio is of the truss-braced section is double the original. With a foldable wing, storage shouldn't be a problem?

Fig. 1, Row 1, L-R Top, bottom; Row 2, L-R front, back; Row 3 L-R, left, right views

     Cruise conditions are taken from [1] i.e. ~12,500 m and ~163.6 m/s. The CFD mesh has 4,892,425 cells out of those, 449,732 are the the surface of the jet. I compare lift/drag of both halves. The modified section produces 36.15% more drag (force) as compared to the original design. The modified section however, produces 49% more lift (force) than the original design. L/D for truss-winged section is at 6.72 as compared to 6.14 for the original design. In terms of L/D, the truss-braced wing section produced 🥁 ... 9.45% more Lift/Drag. A resounding success 😁, I'd say. For validation of CFD, read this and this.

     Some post processing I did, is shown in Fig. 2. Velocity iso-lines with vectors are shown around the wings. Vorticity is shown in the wake of the jet(s). Tip vortex is smaller and less intense behind the truss-braced wing portion but there is another vortex where the truss meets with the main wing. In the main wing, for the trussed-braced portion; on the pressure side; the high pressure zones extend for a longer portion of the span in the span-wise direction as compared to the original design. Same is true for low pressure zones on the suction side of the main wing. Some day I will write a nice little paper and sent it to an AIAA conference, till then 𝌗.

Fig. 2, Colorful Fluid Dynamics 🌈

     Stream-wise vorticity is shown in Fig. 3. It is clear from Fig. 3 that the vorticity is less intense on the side with truss-braced wing as compared to the original design. Fig. 3 is colored by stream-wise velocity. The aircraft appears blue due to no slip condition.

Fig. 3, Some more Colorful Fluid Dynamics (CFD) 🌈

     Thank you for reading, if you would like to hire me as your master's / PhD student / post-doc / collaborate on research projects, please reach out! 😌

References

[1] "Operations Planning Guide". Business & Commercial Aviation. Aviation Week. May 2016. [https://web.archive.org/web/20160815060134/http://www.sellajet.com/adpages/BCA-2016.pdf]

Aperiodic Aero-foil Kinematics

     This post is about a 2D NACA 0012 aero-foil undergoing forced aperiodic heaving. Heaving motion is achieved by the plot shown in Fig. 1. Plot within Fig. 1 represents position of airfoil at various time steps.

Fig. 1, The position of aero-foil

     The animation of the vorticity contours are shown in Fig. 2. The velocity, pressure and vorticity for aperiodic heaving is shown in Fig. 3. A comparison will be made with heaving later, if ever 😀. As far as aerodynamic forces are concerned, per-cycle C_{l, avg} is at 0.63 as compared to 0.0 for periodic heaving. C_{d, avg} aperiodic heaving is at 0.162 as compared to 0.085 for periodic heaving. Of course, this is done on a coarse mesh. If ever I write a paper about this... 😀

Fig. 2, Top Row, Aperiodic, periodic heaving airfoil 

     

Fig. 3, Top Row, L-R, Vorticity, pressure. Bottom Row, Velocity 

     If you want to collaborate on the research projects related to turbomachinery, aerodynamics, renewable energy, please reach out. Thank you very much for reading. 

High Lift Common Research Model (CRM-HL) CFD Simulation (with validation from Stanford CTR and NASA) Update 01: Formation Flight

     This post is about the CFD analysis of the nominal (2A) configuration of the Boeing / NASA CRM-HL with flap and slat angles at 40 and 37 degrees. The configuration is shown in Fig. 1.

Fig. 1, CRM-HL CAD

     The dimensions are mentioned in [1] and is available here and here. The numerical simulations are validated with published literature [3, 4]. SolidWorks Flow Simulation Premium software is employed for the CFD simulations. The flight conditions are Mach 0.2 at 289.444 K and 170093.66 Pa [2].

     Fig. 2 shows the computational mesh along with the computational domain. The surface mesh is also shown with Fig. 2. It can be seen that the mesh is refined in the areas of interests and in the wake of the aircraft to properly capture the relevant flow features. The Cartesian mesh with immersed boundary method, cut-cell approach and octree refinement is used for creating the mesh. The mesh has 6.5 million cells, of which around 0.71 millions cells are at boundary of the aircraft.

     The simulations employ κ-ε turbulence model with damping functions and two-scales wall functions. SIMPLE-R (modified) as the numerical algorithm. Second order upwind and central approximations as the spatial discretization schemes for the convective fluxes and diffusive terms. The software solves the Favre-averaged Navier-Stokes equations to predict turbulent flow. The simulations are performed to predict three-dimensional steady-state flow over the aircraft

Fig. 2, Dashed lines indicate symmetry boundary conditions

     Angle of attack of 7 and 17 degrees are considered. At 7 degree angle of attack, the drag life and moment coefficients are within 6, 8 and 12% of the published data, respectively. For 17 degree angle of attack, the coefficients are within 4, 7, 33% of the published data [3, 4]. On average, the results of the present simulations are within 6% of the published data for force coefficients and within 12% in terms of pitching moment coefficient. The pitching moment coefficient will improve with refinement of the mesh, as shown by [3]; which I will do if ever I convert this into a manuscript 😂. The post processing from CFD simulations is shown in Fig. 3-4. Within Fig. 3, the iso-surfaces represent vorticity in the direction of flow, colored by pressure. The direction of flow is shown by black arrows. Streamlines colored by vorticity are also visible. It can be seen from Fig. 2 that the simulation captures important flow features such as vortex formation very accurately, in such small number of mesh cells. Fig. 4 shows wing of the velocity iso-surfaces colored by vorticity in the direction of flow, focused around the wing.

Fig. 3, Alternating 7 and 17 degree angles of attacks

Fig. 4, Top-Bottom, 17 and 7 degrees angle of attack

     The simulations are solved using 10 of 12 threads of a 4.0 GHz CPU with 32 GB of total system memory of which almost 30 GB remains in use while the simulations are in progress. To solve each angle of attack, 3 hours and 47 minutes are required.

Update 01

     Formation flight simulation is performed with 7.3 million cells (limited by RAM). Symmetry boundary condition is used to simulate only the area of interest. The mesh and computational domain is shown in Fig. 5. Within Fig. 5, dashed lines indicate symmetry boundary condition.

Fig. 5, Airliners in formation flight mesh and computational domain

     The results show that the leading aircraft has 16.52% more drag than the trailing aircraft. The results also show that the the leading aircraft has 5.4% less lift than the trailing aircraft. However, the leading aircraft produces 2.4% more lift than the airliner flying without the trailing aircraft (flying solo). The leading aircraft also produces 3% less drag than the airliner flying solo. These results are at 7 degree angle of attack. Whether these results are fruitful aero-structurally, remains to be seen. The post processing from simulations are shown in Fig, 6.

Fig. 6, Top-Bottom, 17 and 7 degrees angle of attack

     Within Fig. 7, surface plots represent pressure, velocity streamlines indicate vortices, iso-surfaces show vorticity magnitude in the direction of flight.

     Thank you for reading, If you would like to collaborate on projects, please reach out.

References

[1] Doug Lacy and Adam M. Clark, "Definition of Initial Landing and Takeoff Reference Configurations for the High Lift Common Research Model (CRM-HL)", AIAA Aviation Forum, AIAA 2020-2771, 2020 10.2514/6.2020-2771

[2] 4th AIAA CFD High Lift Prediction Workshop Official Test Cases, https://hiliftpw.larc.nasa.gov/Workshop4/OfficialTestCases-HiLiftPW-4-2021_v15.pdf

[3] K. Goc, S., T. Bose and P. Moin, "Large-eddy simulation of the NASA high-lift common research model", Center for Turbulence Research, Stanford University, Annual Research Briefs 2021

[4] 4TH High Lift Workshop Results, ADS, https://new.aerodynamic-solutions.com/news/18

Flapping Aerofoil For Propulsion

     This post is about a 2D NACA 0012 aerofoil undergoing forced flapping motion for propulsion purposes. Heaving motion is achieved by applying a vertical velocity on the aerofoil based on the Eqn. 1. Similarly the pitching motion is achieved by applying a rotational velocity, governed by Eqn. 2.

v_y = 2*π*f_h*H_o*sin(2*π*f_h*t)                                              Eqn. 1

ω = -2*π*f_h*ϑ*sin[(2*π*f_h*t) + 1.5708]                               Eqn. 2

     w.r.t. Eqn. 1-2 reduced frequency is defined as (2*π*f_h*H_o/U∞)), f_h is the frequency of oscillations, while ω, t and ϑ_o represent rotational velocity, instantaneous time and maximum pitching angle. H_o is the heaving amplitude and U∞ is the free stream velocity.

     The flapping motion is achieved by a combination of the heaving and pitching. In this particular simulation, the aerofoil is in the propulsion mode, meaning the feathering parameter χ is less in magnitude than 1.0. Feathering parameter is defined by Eqn. 3.

χ = ϑ/arctan(h0*2*π*f_h/U∞)                                  Eqn. 3

     The boundary conditions employed for the simulation are at Re 1,000, K = 1.41, H_o = aerofoil chord length, χ = 0.5489 and f_h = 0.003391 Hz. The animation of the pressure, vorticity and velocity contours is shown in Fig. 1.

Fig. 1, Flow animation, fluid flow direction is from left to right.

     The results of present simulation are compared with [1]. In terms of maximum lift, a maximum deviation of 5% is observed as compared to [1], as shown in Fig. 2. The maximum lift coefficient for available data is ~4.224 while the maximum lift coefficient from the present simulation is ~4.057. The average thrust produced is within 2% of [1]. Average thrust coefficient per cycle from [1] is 0.9957 while the result from present simulation reveals the thrust coefficient to be 1.0098.

Fig. 2, A comparison of coefficient of lift.

If you want to collaborate on the research projects related to turbo-machinery, aerodynamics, renewable energy, please reach out. Thank you very much for reading.

References

[1] https://doi.org/10.1017/jfm.2017.508

Aerofoil Kinematics Computational Fluid Dynamics (Update: 01)

This post is about a 2D NACA 0010 aerofoil undergoing various forms of forced kinematics i.e. pure heaving and pitching and a combination of two known as flapping.

Heaving motion is achieved by changing the angle of attack on the aerofoil based on the Eqn. 1.

α_e = arctan[2*π*St_a*cos(2*π*f_h*t)] + α_i               Eqn. 1

The pitching motion is achieved by employing the sliding mesh with the rotational velocity governed by Eqn. 2.

ω = 2*π*f_h*ϑ*cos(2*π*f_h*t)                                 Eqn. 2

w.r.t. Eqn. 1-2 α_e is the effective angle of attack, St_a is Strouhal number (defined as (f_h*h0/U∞)), f_h is the frequency of oscillations, while ω, t and ϑ represent rotational velocity, instantaneous time and pitching angle. h0 is the heaving amplitude and U∞ is the free stream velocity.

The flapping motion is achieved by a combination of the heaving and pitching. In this particular simulation, the aerofoil is in the power extraction mode, meaning the feathering parameter χ is greater in magnitude than 1.0. Feathering parameter is defined by Eqn. 3.

χ = ϑ/arctan(h0*2*π*f_h/U∞)                                  Eqn. 3

The boundary conditions employed for the set of simulations are at Re 50,000, St_a 0.0149, h0 = aerofoil chord length, χ = 1.1 and f_h = 0.5 Hz. The animation of the velocity contours superimposed with streamlines is shown in Fig. 1. The velocity scale ranges from 0 to 7 m/s. Pressure distribution around the aerofoils in various forms of motion, after five complete cycles is shown in Fig. 2.

Fig. 1, Flow animation, fluid flow direction is from left to right

Fig. 2, Fluid flow is from left to right

If you want to collaborate on the research projects related to turbomachinery, aerodynamics, renewable energy, please reach out. Thank you very much for reading.

Heaving Airfoil Simulation

This post is about a 2D NACA 0012 heaving aerofoil. Heaving motion is achieved by changing the angle of attack on the aerofoil based on the Eqn. 1.

α_e = arctan[2*π*St_a*cos(2*π*f_h*t)]+ α_i               Eqn. 1

w.r.t. Eqn. 1, α_e is the effective angle of attack, St_a is Strouhal number, f_h is the heaving frequency.

The case S1 and H6 from [1] are compared in the animations below.

If you want to collaborate on the research projects related to turbomachinery, aerodynamics, renewable energy, please reach out. Thank you very much for reading.

References

[1] https://doi.org/10.1121/10.0001419

Formation Flight Computational Fluid Dynamics

     This is a post about computational fluid dynamics analysis of formation flight.

     The results from an analysis of three unmanned combat aerial vehicles (UCAVs) flying in a V-type formation are presented. The chosen UCAV configuration, shown in Figs. 1-2 and available for download here, is named SACCON (Stability And Control Configuration) UCAV. This configuration is used because of the availability of the geometric and aerodynamic data, used in the validation and verification of the numerical analysis. The SACCON UCAV is designed by NATO's (North Atlantic Treaty Organization) RTO (Research and Technology Group) under Applied Vehicle Task Group (AVT-161) to assess the performance of military aircrafts.

Fig. 1, SACCON UCAV

Fig. 2, Technical drawing for the SACCON UCAV

     The simulation is performed using commercially available computational fluid dynamics code.  The details about the solver and the discretization schemes are presented next. The simulation is performed using SIMPLE-R solver for pressure-velocity coupling. The diffusive terms of the Navier-Stokes equations are discretized using central differentiating scheme while the convective terms are discretized using the upwind scheme of second order. The κ-ε turbulence model with damping functions is implemented to model turbulence. The simulation predicts three-dimensional steady–state flow over UCAVs.

     The Reynolds and Mach number of flow are set at 1e6 and 0.15, respectively. The two trailing UCAVs are placed 3 wingspans behind the leading UCAV. The trailing UCAVs are a wingspan apart. The V-type configuration is chosen because it is the most common observation in birds (author's observation). The V-type formation is shown in Fig. 3. All three UCAVs are at 5° angle-of-attack.

Fig. 3, The V-type formation (top view)

     The boundaries of the computational domain are located at a distance equivalent to 10 times the distance between the nose of the leading UCAV and the tail of the trailing UCAV. The mesh is made of 821,315 cells. Mesh controls are used to refine the mesh in the areas of interest i.e. on the surfaces of the UCAVs and in the wake of all three UCAVs. A cartesian mesh with immersed boundary method is used for the present study. The computational domain with mesh is shown in Fig. 4 while a closeup of the mesh is shown in Fig. 5.

Fig. 4, The computational domain and mesh

Fig. 5, Closeup of mesh, notice the refined wakes of the UCAVs

     For validation and verification, the lift and drag forces from the present study are compared with studies [1-2]. The results are in close agreement with [1,2] As a result of flying in a formation, an improvement in the lift-to-drag ratio of 10.05% is noted. The lift-to-drag ratio of the trailing UCAVs is at 11.825 in comparison with a lift-to-drag ratio of a single UCAV, i.e. 10.745. The lift coefficient is increased by 7.43% while the drag coefficient decreased by 2.174%. The reason(s) to why the efficiency increases will be looked upon later, if ever the author has the time and will power ☺.

     The results from post processing of the simulations are presented in Figs. 6-7. The pressure iso-surfaces colored by velocity magnitude are shown in Fig. 6. While the velocity iso-surfaces colored by pressure magnitude are shown in Fig. 7.

Fig. 6, Flight direction towards the reader

Fig. 7, Flight direction away from the reader

     Thank you very much for reading. If you would like to collaborate on research projects, please reach out.

[1] https://doi.org/10.2514/1.C031386

[2] https://doi.org/10.1155/2017/4217217

High Camber Wing CFD Simulation

     This post is about the numerical simulation of a high camber, large aspect ratio wing. The wing had an aspect ratio of 5:1. The Reynolds number of flow was 500,000. The wing was at an angle of attack of zero degree. The aero-foil employed had a cross section of NACA 9410.

     The software employed was Flow Simulation Premium. A Cartesian mesh was created using the immersed boundary method. The mesh had 581,005 cells. Among those 581,005 cells, 55,882 were at the solid-fluid boundary. A time step of ~0.00528167 s was employed*. The domain was large enough to accurately trace the flow around the wing without any numerical or reversed flow errors. The software employs κ-ε turbulence model with damping functions, SIMPLE-R (modified) as the numerical algorithm and second order upwind and central approximations as the spatial discretization schemes for the convective fluxes and diffusive terms. The time derivatives are approximated with an implicit first-order Euler scheme.

     The mesh is shown in Fig. 1. The four layers of different mesh density are also visible in Fig. 1, the mesh is refined near the wing surface using a mesh control. The velocity around the wing section is shown in Fig. 2, using a cut plot at  the center of the wing. In Fig. 2, the wing body is super imposed by pressure plot. The velocity vectors showing the direction of flow are superimposed on both the wing body and the velocity cut plot.

Fig. 1, The computational domain.

Fig. 2, The velocity and pressure plots.

     The results of the simulation was validated against the results from XFLR5 software. XFLR5 predicted slightly higher lift and slightly less drag on the wing for same boundary conditions because the XFLR5 simulations were inviscid.

     Thank you for reading. If you would like to contribute to the research, both financially and scientifically, please feel free to reach out.

     *Time step is averaged because of the fact that a smaller time step was employed at the start of the numerical simulation.

11x7 Aeronautic Propeller Characteristics (Using CFD) (Verified and Validated) (Update 02)

     This post presents the results from an aeronautic propeller CFD analysis.

    
     An 11x7 propeller was modelled using SolidWorks CAD package using the geometry from [1]. The simulations were run at two different rotational velocities and each rotational velocity was simulated at three advance ratios. The mesh for the 3,000 RPM rotational velocity had 213,205 total cells among which 24,048 cells were at the solid fluid boundary. While, the mesh for the 5,000 RPM rotational velocity had 369,963 total cells among which 68,594 cells were at the solid fluid boundary. A mesh control was employed to refine the mesh near the propeller geometry and at the boundary of the rotating region and the stationery domain for all of the cases simulated. This was done to ensure accuracy of the results was within an acceptable range. The results of the numerical simulations are plotted along with the experimental results [1] in Fig. 1.

Fig. 1 J= Advance Ratio, η_prop = propeller efficiency

     It can be seen from Fig. 1 that the trends for the propeller efficiency are in agreement with the experimental results. To increase the mesh density for the mesh independence test, the number of cells in  each of the respective co-ordinate directions was increased by a factor of 1.1. The mesh is shown in the Fig. 2.

Fig. 2 The computational mesh around the propeller.

     The computational domain size was at 2D x 2D x 2.4D, D being the propeller diameter, as shown in Fig. 3. In Fig. 3, the curved teal arrow represents the direction of rotation of the sliding mesh. The blue arrow represents the direction of free stream velocity while the brown arrow represents the force of gravity.

 Fig. 3 The computational domain.

Fig. 4 The pressure distribution and the velocity vectors around the propeller.

     The CAD model files and the simulation setup files for the numerical analysis are available here.

     Thank you for reading. If you'd like to collaborate on research projects, please reach out.

[1] Brandt, J. B., & Selig, M. S., “Propeller Performance Data at Low Reynolds Numbers,” 49th AIAA Aerospace Sciences Meeting, AIAA Paper 2011-1255, Orlando, FL, 2011.

doi.org/10.2514/6.2011-1255

 

Update 01

     Results from the mesh independent study are now available.

Update 02

     CAD model files are now uploaded. The CFD simulation setup files are also included.

11x4.7 Aeronautic Propeller Characteristics (Using CFD) (Verified and Validated) (Update 02)

     This post presents the results from an aeronautic propeller CFD analysis.

     An 11x4.7 propeller was modelled using SolidWorks CAD package using the geometry from [1]. The simulations were run at two different rotational velocities and each rotational velocity was simulated at three advance ratios. The mesh for the 3,000 RPM rotational velocity had 206,184 total cells among which 22,103 cells were at the solid fluid boundary. While, the mesh for the 6,000 RPM rotational velocity had 357,300 total cells among which 64,012 cells were at the solid fluid boundary. A mesh control was employed to refine the mesh near the propeller geometry and at the boundary of the rotating region and the stationery domain for all of the cases simulated. This was done to ensure accuracy of the results was within an acceptable range. The results of the numerical simulations are plotted along with the experimental results [1] in Fig. 1.

Fig. 1 J= Advance Ratio, η_prop = propeller efficiency

 

     It can be seen from Fig. 1 that the trends for the propeller efficiency are in agreement with the experimental results. The fine mesh had the number of cells in each of the respective co-ordinate directions increased by a factor of 1.1. The mesh is shown in the Fig. 2.

 

Fig. 2 The computational mesh around the propeller.

 

     The computational domain size was at 2D x 2D x 2.4D, D being the propeller diameter, as shown in Fig. 3. In Fig. 3, the curved teal arrow represents the direction of rotation of the sliding mesh. The blue arrow represents the direction of free stream velocity while the brown arrow represents the force of gravity.

Fig. 3 The computational domain.

Fig. 4 The pressure distribution and the velocity vectors around the propeller.

     The CAD model and numerical simulation setup files are available here.

 

     Thank you for reading. If you'd like to collaborate on research projects, please reach out.

     [1] Brandt, J. B., & Selig, M. S., “Propeller Performance Data at Low Reynolds Numbers,” 49th AIAA Aerospace Sciences Meeting, AIAA Paper 2011-1255, Orlando, FL, 2011.

doi.org/10.2514/6.2011-1255

 

Update 01

     Mesh independent test results are now available.

 

Update 02

     CAD files for the propeller including the CFD analysis setup are now available.

Marine Propeller Characteristics (Using CFD) (Verified and Validated)

     This post presents the results from a marine propeller CFD analysis. The key thing about this CFD analysis was that the propeller efficiency obtained was within 7% of the experimental results, by using only 112,081 total cells in the computational mesh, of these cells, 21,915 cells were at the solid fluid boundary. The results are, indeed, mesh independent. The software employed was Flow Simulation Premium. The results of the numerical simulations are plotted along with the experimental results in Fig. 1.

Fig. 1 K_T = coefficient of thrust, 10K_Q = coefficient of torque multiplied by a factor of 10, η_prop = propeller efficiency

 

     It can be seen from Fig. 1 that the trends for the thrust and the torque coefficients and the propeller efficiency are in agreement with the experimental results. The experimental data was taken from here. The flow conditions were following. The propeller diameter was at 0.254 m. Propeller rotational velocity was at 15 rev/s. The propeller inclination angle was at 12°. Fluid considered was water. To change the advance ratio, fluid flow velocity was altered. The computational domain size was at 2D x 2D x 3.2D, D being the propeller diameter, as shown in Fig. 3. The mesh is shown in the Fig. 2.

Fig. 2 The computational mesh around the propeller.

 

Fig. 3 The computational domain.

 

     In Fig. 3, the curved teal arrow represents the direction of rotation of the sliding mesh. The blue arrow represents the direction of free stream velocity while the brown arrow represents the force of gravity. The Pressure distribution on the propeller blades and the velocity streamlines are shown in Fig. 4. The streamlines were drawn using line integral convolution, relative to the rotating frame of reference.

 

Fig. 4 The pressure distribution and the velocity profile around the propeller.

 

     If you'd like to collaborate on research projects, please reach out. Thank you for reading.