Yours truly is an avid gamer, @fadoobaba (YouTube). The ray casting algorithm🛸; a fundamental 🧱 technique used in video game 🎮 development and computer graphics, has been implemented within the finite difference method 🏁 code yours truly has been developing. In abundant spare time, of course😼. In this post, this method is explained. For details about ray casting using matplotlib.path, refer to here. For validation of the code, refer to here, backwards-facing step, curved boundaries, here (moving cylinder) and here.
NOTE: This method requires a GPU, if dear readers don't have a GPU then please stop being peasants... 🙉
If you plan to use these codes in your scholarly work, do cite this blog as:
Fahad Butt (2025). S-IBM (https://fluiddynamicscomputer.blogspot.com/2025/07/a-simplified-immersed-boundary-method.html), Blogger. Retrieved Month Date, Year
The first step is to setup the polygon 🐠. The polygon = cp.column_stack((x1, y1)) statement is used to combine x1 and y1 into a single array representing the polygon vertices. The following statements are used to store the x and y coordinates of the polygon vertices and nvert is the total number of vertices.
px = polygon[:, 0]
py = polygon[:, 1]
nvert = len(polygon)
The boolean masks 👺 are then initialized. The following arrays track whether a grid point is inside the polygon based on horizontal and vertical ray intersections. False = outside ❌, True = inside ✅. Then a loop is implemented to for each edge 📏 of the polygon, defined by vertices i (current) and j (previous), with % nvert ensuring the polygon is closed (last vertex connects back to the first). (xi, yi) and (xj, yj) define the current edge and previous edge.
vertical_inside = cp.zeros_like(test_x, dtype=bool)
for i in range(nvert):
j = (i - 1) % nvert
xi, yi = px[i], py[i]
xj, yj = px[j], py[j]
A check ⁉️ is performed to ensure a ray crosses the polygon edge once. cond1 statement checks if the test point lies between the y-values of the edge's endpoints i.e., a ray could cross it. intersect_x finds where the edge crosses a horizontal line at test_y. cond2 checks if the intersection lies to the right of the test point. ^= is XOR toggles the "inside" state each time the ray crosses an edge. The addition of small term ~1e-16 prevents division by zero for horizontal edges. Similar method is applied to verify the points using vertical ray. cond3 checks if the edge crosses a vertical ray (top to bottom) from (test_x, test_y). slope1 and intersect_y computes where the vertical ray at x=test_x intersects the edge. A point is inside only if both horizontal and vertical rays classify it as inside. A point is considered inside the foil only if both ray checks are true. curve is the 2D boolean mask of grid points inside the foil body.
cond1 = ((yi > test_y) != (yj > test_y))
slope = (xj - xi) / (yj - yi + 1e-16)
intersect_x = slope * (test_y - yi) + xi
cond2 = test_x < intersect_x
horizontal_inside ^= cond1 & cond2
cond3 = ((xi > test_x) != (xj > test_x))
slope1 = (yj - yi) / (xj - xi + 1e-16)
intersect_y = slope1 * (test_x - xi) + yi
cond4 = test_y < intersect_y
vertical_inside ^= cond3 & cond4
inside = horizontal_inside & vertical_inside
curve = inside.reshape(X.T.shape)
Using both horizontal and vertical rays reduces false positives (e.g., near sharp corners). The & ensures only points unambiguously inside are marked. Within Fig. 1, the points on the shape boundary, points inside 🪰 and outside 🐌 the shape boundary are shown. A point is a boundary if it is inside the body, but any of its neighbors is outside. Following statements are used to mark the boundary of the object. Boundary detects the "skin" of the body for applying no-slip, force, or stress conditions.
right = curve[2:, 1:-1]
left = curve[:-2, 1:-1]
top = curve[1:-1, 2:]
bottom = curve[1:-1, :-2]
boundary = interior & ~(right & left & top & bottom)
 |
| Fig. 1, Mesh cells |
For validation of the results from present simulations, the case of flow around a circular cylinder is selected. Fig. 1 shows the results from the code at Re 200. The drag coefficient obtained from this code is 1.396 while from the literature, the value is at 1.4 [1]. The lift coefficient from the code is at 0.000134. Within Fig. 2, top row shows u and v velocity components and bottom row shows pressure and vorticity.
 |
| Fig. 2, The flow-field |
For the second an more complex validation case, a swimming fish is simulated. The lift and drag coefficients obtained from the simulation are compared with experimental results. The drag coefficient from the current code is at 0.342 while from the published literature, the value is at 0.348. Maximum lift coefficient is at 7.243 and 8 from the present code as compared to the published literature [2]. Within Fig. 3 the u and v velocities, pressure and velocity streamlines are shown for St = 0.8 and Reynolds number of 500. The computational mesh near the fish is shown in Fig. 4. Within Fig.4, a zoomed in view towards the right shows the mesh at the trailing edge of the fish.
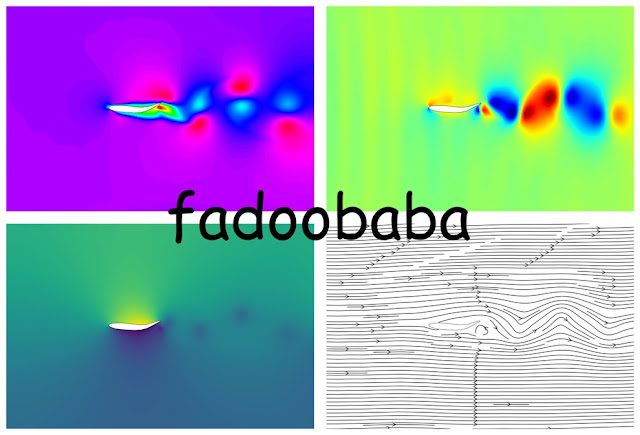 |
| Fig.3, Post-processing of results |
 |
| Fig. 4, The mesh |
This method allows handling arbitrary deforming / non-deforming shapes on a fixed Cartesian grid. In summary, the method has the following steps.
1. Generate polygon shape (e.g., airfoil, cylinder)
2. Flatten mesh for vectorized testing
3. Use ray casting to check if points are inside shape
4. Build a boolean mask of body region
5. Identify surface (boundary) points
6. Extract boundary indices for physics coupling
Hi is there anyway to contact you?
ReplyDeleteHello! Thank you for your interest. What do you want to ask?
Delete