Numerical simulations were run on SolidWorks Flow Simulation Premium (model files are available
here) software to compare the torque characterizes of three distinct vertical-axis wind turbine blade designs shown in Fig. 1. The torque characteristics are shown in Fig. 2.
This
publication was used to verify and validate the numerical methodology. The results were within 8% of the publication's results at the design point of TSR of 1.2 at 90 RPM and 7.85 m/s wind speed. The dimensions of the turbine, the blades and the cross section used are mentioned in the publication.
Fig. 1. Top Row, L-R: VAWT with blades having tubercles at the leading edge (ten tubercles per blade span, configuration name 10T), VAWT with blades having tubercles at both the leading and the trailing edge (ten tubercles per blade span). Bottom Row, VAWT with blades having no modifications.
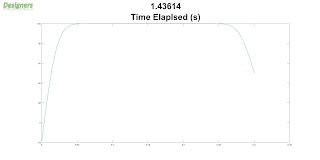
It is clear from the Fig. 2 that the baseline design provides the most stable torque. On average the turbine with no modifications on the blades produced 5.31 Nm torque in one complete rotation, while the turbine with tubercles at the leading edge only, produced 5.20 Nm torque. The turbine with tubercles added to both the leading and the trailing edge produced 5.09 Nm torque in one complete rotation.
The peak torque was maximum for the turbine with the leading edge tubercles, followed by the turbine with the tubercles added to both the leading and the trailing edge of the turbine blades and the turbine with no modifications on the blades at 21.59 Nm, 21.45 Nm and 20.58 Nm respectively.
Fig. 2. Top Row, L-R: Torque curves for VAWT with blades having tubercles at the leading edge, Torque curves for VAWT with blades having tubercles at both the leading and the trailing edge. Bottom Row, Torque curves for VAWT with blades having no modifications. Three colors denote each of the blades in the turbine.
CFD post processing will be added later (may be next week). The effect of leading edge tubercle geometry will be investigated next. The blade design with tubercles added to both the leading and the trailing edge will not be investigated further because it produced the lowest average torque and second highest peak torque.
Update 01:
Decreased the number of tubercles per unit length of the blade, i.e. made the wavelength of the tubercles longer, kept the sweep angle same. As a result, the average and peak torque decreased to 4.53 Nm, and 19.33 Nm, respectively. The figure is attached.
Fig. 3. T-B: Torque curves for VAWT with blades having large wavelength tubercles at the leading edge (five tubercles per blade span, configuration name 5T45). Three colors denote each of the blades in the turbine. Render of the blades.
Update 02:
Increased the number of tubercles per blade span, i.e. made the wavelength of the tubercles smaller, kept the sweep angle same. As a result, the average and peak torque increased to 5.80 Nm, and 23.36 Nm, respectively. The figure is attached.
Fig. 4. T-B: Torque curves for VAWT with blades having smaller wavelength tubercles at the leading edge (fifteen tubercles per blade span, configuration name 15T45). Three colors denote each of the blades in the turbine. Render of the blades.
Update 03:
Again, increased the number of tubercles per blade span, i.e. made the wavelength of the tubercles smaller, kept the sweep angle same. As a result, the average and peak torque increased to 6.1 Nm, and 24.12 Nm, respectively. The figure is attached.
Fig. 5. T-B: Torque curves for VAWT with blades having smaller wavelength tubercles at the leading edge (twenty tubercles per blade span, configuration name 20T45). Three colors denote each of the blades in the turbine. Render of the blades.
Update 04:
Once more, increased the number of tubercles per blade span, i.e. made the wavelength of the tubercles smaller, kept the sweep angle same. As a result, the average and peak torque increased to 6.42 Nm, and 24.63 Nm, respectively. The figure is attached.
Fig. 6. T-B: Torque curves for VAWT with blades having smaller wavelength tubercles at the leading edge (twenty-five tubercles per blade span, configuration name 25T45). Three colors denote each of the blades in the turbine. Render of the blades.
A table for the tubercle geometry is shown below.
Table 01, Tubercle Geometry
Configuration Name
|
Amplitude (m)
|
Wavelength (m)
|
Sweep Angle (°)
|
Baseline
|
0
|
0
|
0
|
5T45
|
0.12777778
|
0.25555556
|
45
|
10T45
|
0.06052632
|
0.12105263
|
45
|
15T45
|
0.03965517
|
0.07931034
|
45
|
20T45
|
0.02948718
|
0.05897436
|
45
|
25T45
|
0.02346939
|
0.04693878
|
45
|
It is evident from Table 2 that adding more tubercles to the wind turbine's blade causes an increase in both the peak and the average torque. But it is also clear from the Table 2 that the percentage difference in both the average and the peak torque from the previous configuration (less tubercles per blade span) decreases as the number of tubercles per blade span is increased. It appears to be converging to a value.
Table 02, Tubercle Efficiency
Configuration Name
|
Peak Torque (Nm)
|
Average Torque (Nm)
|
Percentage Difference in the Average Torque from the Previous
Configuration
|
Percentage Difference in the Average Torque from then Baseline
Configuration
|
Baseline
|
20.58
|
5.31
|
N/A
|
N/A
|
5T45
|
19.33
|
4.53
|
-17.22
|
-17.22
|
10T45
|
21.59
|
5.2
|
12.89
|
-2.12
|
15T45
|
23.36
|
5.8
|
10.35
|
8.45
|
20T45
|
24.12
|
6.1
|
4.92
|
12.95
|
25T45
|
24.63
|
6.42
|
4.98
|
17.29
|
I think the difference between both the peak and the average torque produced by 25T45 and 20T45 configuration is comparable, up next, a new sweep angle.
Update 05
Following are my publications relating to the subject of this post.
Butt, F.R., and Talha, T., "A Numerical Investigation of the Effect of Leading-Edge Tubercles on Propeller Performance," Journal of Aircraft. Vol. 56, No. 2 or No. 3, 2019, pp. XX. (Issue/page number(s) to assigned soon. Active DOI: https://arc.aiaa.org/doi/10.2514/1.C034845)
Butt, F.R., and Talha, T., "A Parametric Study of the Effect of the Leading-Edge Tubercles Geometry on the Performance of Aeronautic Propeller using Computational Fluid Dynamics (CFD)," Proceedings of the World Congress on Engineering, Vol. 2, Newswood Limited, Hong Kong, 2018, pp. 586-595, (active link: http://www.iaeng.org/publication/WCE2018/WCE2018_pp586-595.pdf).
Butt, F.R., and Talha, T., "Optimization of the Geometry and the Span-wise Positioning of the Leading-Edge Tubercles on a Helical Vertical-Axis Marine Turbine Blade ," AIAA Science and Technology Forum and Exposition 2019, Turbomachinery and Energy Systems, accepted for publication.
Thank you for reading.