The adventure 🏕 🚵 I started a while ago to make my own CFD 🌬 code / software 💻 for my digital CV and to make a shiny new turbulence mode (one-day perhaps) is going along nicely. This post is about a 2D 10% flat plate undergoing forced heaving motion. Heaving motion is achieved by Eqn. 1.
I write about Propulsion, Aerodynamics and Renewable Energy (Wind/Hydro Turbines).
Monday, 14 August 2023
Heaving Flat Plate Computational Fluid Dynamics (CFD) Simulation (In-House CFD Code)
Saturday, 22 July 2023
Home-Made Computational Fluid Dynamics (CFD), (Includes CFD code)
One fine morning, I decided to code the Navier–Stokes equations using the finite-difference method. This post has the results of this adventure 🏞️ (so-far). As is customary with all my CFD work using commercial and home-made CFD codes, this too is inspired by the free lectures of Dr. Lorena Barba.
Internal / External Fluid Dynamics - Lid-Driven Cavity
I started using Lid-Driven Cavity example. Just because everyone else uses it to validate the code they write. The lid-driven cavity case is giving correct results up to ~Re 1,000 without any turbulence models or wall functions.
The results shown in Fig. 1 correspond to at Re 1,000. It can be seen that the present code which is just vanilla Navier–Stokes; captures the vortices at both bottom edges well as compared to published data. But why would you want to use a vanilla CFD code which solved only ~Re 1,000?, anyways... Some validation... u-velocity at (0.5, 0.1719) is at -0.3869 m/s as compared to -0.38289 m/s [1]. Meanwhile, v-velocity at (0.2266, 0.5) is 0.3252 as compared to 0.30203. Furthermore, v-velocity at (0.8594, 0.5) is at -0.4128 m/s as compared to -0.44993 m/s. All in all, a good agreement with published data. An animation is uploaded here. Fig. 1a shows a different variation of lid driven cavity.
 |
| Fig. 1, Lid driven cavity post-processing |
 | |
|
Internal / External Aerodynamics - Backward-Facing Step (BFS)
 |
| Fig. 2, Backward Facing Step (BFS) post processing at Re 200 |
Internal Fluid Dynamics - Aero-Thermal Pipe Flow
 |
| Fig. 3, Flow through heated pipe / between flat plates |
Clot Flow
 |
| Fig. 4, Flow inside a blood vessel with and without clot |
External Aerodynamics - Flow around a Square Cylinder
Why not circular cylinder you ask? I am very lazy 😂. It is hard work to draw a circle using code. I am used to CAD. 😇. Again, low Reynolds number are very rare in practical applications but for the sake of completeness, I added this case as well. Fig. 5 shows flow around the cylinder at Re 100. Vorticity is shown in Fig. 5. The results are compared with experimental data. The Strouhal number from the home-made CFD code is at 0.158 as compared to a value of 0.148. The results are within 7% of published literature [2-3].
 |
| Fig. 5, Post-processing |
Thank you for reading! If you want to hire me as your most awesome PhD student, please reach out!
Code:
I present to you the code-able discretized equations for solving fluid flow problems. At first, C++ version is presented followed by the MATLAB version. Equation 1-2 are Poisson equations for pressure. Equation 3 and 4 are x-momentum equations (without source). Equations 5 and 6 are y-momentum equations.
double p_ij = ((pn(i + 1, j) + pn(i - 1, j)) * dy * dy + (pn(i, j + 1) + pn(i, j - 1)) * dx * dx) / (2 * (dx * dx + dy * dy)) - dx * dx * dy * dy / (2 * (dx * dx + dy * dy)) * (rho * (1 / dt * ((u(i + 1, j) - u(i - 1, j)) / (2 * dx) + (v(i, j + 1) - v(i, j - 1)) / (2 * dy)) - ((u(i + 1, j) - u(i - 1, j)) / (2 * dx)) * ((u(i + 1, j) - u(i - 1, j)) / (2 * dx)) - 2 * ((u(i, j + 1) - u(i, j - 1)) / (2 * dy) * (v(i + 1, j) - v(i - 1, j)) / (2 * dx)) - ((v(i, j + 1) - v(i, j - 1)) / (2 * dy)) * ((v(i, j + 1) - v(i, j - 1)) / (2 * dy)))); (1)
p(i, j) = ((pn(i+1, j) + pn(i-1, j)) * dy^2 + (pn(i, j+1) + pn(i, j-1)) * dx^2) ./ (2 * (dx^2 + dy^2)) - dx^2 * dy^2 / (2 * (dx^2 + dy^2)) * (rho * (1/dt * ((u(i+1, j) - u(i-1, j)) / (2 * dx) + (v(i, j+1) - v(i, j-1)) / (2 * dy)) - ((u(i+1, j) - u(i-1, j)) / (2 * dx)).^2 - 2 * ((u(i, j+1) - u(i, j-1)) / (2 * dy) .* (v(i+1, j) - v(i-1, j)) / (2 * dx)) - ((v(i, j+1) - v(i, j-1)) / (2 * dy)).^2)); (2)
double u_ij = un(i, j) - un(i, j) * dt / dx * (un(i, j) - un(i - 1, j)) - vn(i, j) * dt / dy * (un(i, j) - un(i, j - 1)) - dt / (2 * rho * dx) * (p(i + 1, j) - p(i - 1, j)) + nu * (dt / (dx * dx) * (un(i + 1, j) - 2 * un(i, j) + un(i - 1, j)) + dt / (dy * dy) * (un(i, j + 1) - 2 * un(i, j) + un(i, j - 1))); (3)
u(i, j) = un(i, j) - un(i, j) * dt/dx .* (un(i, j) - un(i-1, j)) - vn(i, j) * dt/dy .* (un(i, j) - un(i, j-1)) - dt / (2 * rho * dx) * (p(i+1, j) - p(i-1, j)) + nu * (dt/dx^2 * (un(i+1, j) - 2 * un(i, j) + un(i-1, j)) + (dt/dy^2 * (un(i, j+1) - 2 * un(i, j) + un(i, j-1)))); (4)
double v_ij = vn(i, j) - un(i, j) * dt / dx * (vn(i, j) - vn(i - 1, j)) - vn(i, j) * dt / dy * (vn(i, j) - vn(i, j - 1)) - dt / (2 * rho * dy) * (p(i, j + 1) - p(i, j - 1)) + nu * (dt / (dx * dx) * (vn(i + 1, j) - 2 * vn(i, j) + vn(i - 1, j)) + dt / (dy * dy) * (vn(i, j + 1) - 2 * vn(i, j) + vn(i, j - 1))); (5)
v(i, j) = vn(i, j) - un(i, j) * dt/dx .* (vn(i, j) - vn(i-1, j)) - vn(i, j) * dt/dy .* (vn(i, j) - vn(i, j-1)) - dt / (2 * rho * dy) * (p(i, j+1) - p(i, j-1)) + nu * (dt/dx^2 * (vn(i+1, j) - 2 * vn(i, j) + vn(i-1, j)) + (dt/dy^2 * (vn(i, j+1) - 2 * vn(i, j) + vn(i, j-1)))); (6)
Of course constants need to be defined, such as grid spacing in space and time, density, kinematic viscosity. These equations have been validated, as you might have read already! Happy coding!
If you want to hire me as your PhD student in the research projects related to turbo-machinery, aerodynamics, renewable energy, please reach out. Thank you very much for reading.
References
[1] U Ghia, K.N Ghia, C.T Shin, "High-Re solutions for incompressible flow using the Navier-Stokes equations and a multigrid method", Journal of Computational Physics, Volume 48, Issue 3, 1982, Pages 387-411, ISSN 0021-9991, https://doi.org/10.1016/0021-9991(82)90058-4
[2] Khademinejad, Taha & Talebizadeh Sardari, Pouyan & Rahimzadeh, Hassan. (2015). Numerical Study of Unsteady Flow around a Square Cylinder in Compare with Circular Cylinder
[3] Ávila, Ítalo & Santos, Gabriel & Ribeiro Neto, Hélio & Neto, Aristeu. (2019). Physical Mathematical and Computational Modeling of the Two-Dimensional Flow Over a Heated Porous Square Cylinder. 10.26678/ABCM.COBEM2019.COB2019-0854
[4] Irisarri, Diego & Hauke, Guillermo. (2019). Stabilized virtual element methods for the unsteady incompressible Navier–Stokes equations. Calcolo. 56. 10.1007/s10092-019-0332-5.
Monday, 10 July 2023
CFD Basics: Code Vectorization
This post is about comparing 2 codes to solve the 2D Laplace equation using finite difference method. A sample code mentioned under "Code 01" uses nested loops. We must, wherever possible avoid nested loops. The solution to the code is shown in Fig. 1. The second code uses vectorization instead of the nested loops. The vectorized version is mentioned under "Code 02".
Code 01
Code 02
Result
 |
| Fig. 1, Vectorized VS Nested Loops |
Monday, 17 April 2023
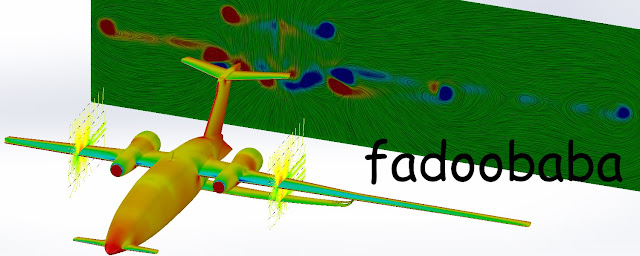
Executive transport aircraft with truss-braced wing (World's First)
To explore large-er aspect ratio wings; one fine morning, I just thought it would be fun to put a truss-braced wing in a Piaggio P.180 "Avanti". The modified design CAD files are is available here. A comparison is shown in Fig. 1. I am too lazy to make 2 separate airplanes so I modified half of it so I can run a CFD analysis using one model and one mesh 🤣. A slight modification about which I will write later is the positioning of the flaps and ailerons. These are moved to the truss part from the main wing in the original design. The aspect ratio is of the truss-braced section is double the original. With a foldable wing, storage shouldn't be a problem?