Wednesday, 12 August 2026

21st Step of the 12 steps to Navier-Stokes 😑 (3D Backwards Facing Step)

Backwards facing step is the simplest case in external aerodynamics. In this post, the code is configured to simulate the case of flow around a 3D backwards facing step. The code 🖳 shared in this post is fully vectorized 😲. Steps 13 to 20 are available here. 13, 14, 15, 16, 17, 18, 19, 20. A thorough validation of the 2D code is available here and here. 🤓

NOTE: This method requires a GPU, if dear readers don't have a GPU then please stop being peasants... 🙉

If for some reason (why? 😁), you plan to use these codes in your scholarly work, do cite this blog as:

Fahad Butt (2026). S-IBM (), Blogger. Retrieved Month Date, Year

Literally, everyone else uses this case to validate the code they write. The case is solved at Re 200 without any turbulence models or wall functions. This code is a simple 3D extension of this code. The code is almost double in length as the 3D version requires under-relaxation and has one more momentum equation. In less than 150 lines, flow around the backwards facing step can be simulated with excellent accuracy. The code is available here.

#%% import libraries

import cupy as cp

import matplotlib.pyplot as plt

#%% define parameters

l_cr = 1 # characteristic length

h = l_cr / 100 # grid spacing

dt = 0.001 # time step

L = 9 # domain length

D = 1 # domain width

W = 2 # domain depth

Nx = round(L / h) # grid points in x-axis

Ny = round(D / h) # grid points in y-axis

Nz = round(W / h) # grid points in z-axis

nu = 1 / 200 # kinematic viscosity

Uinf = 1 # free stream velocity / inlet velocity / lid velocity

cfl = dt * Uinf / h # cfl number

travel = 1 # times the disturbance travels entire length of computational domain

TT = travel * L / Uinf # total time

ns = int(TT / dt) # number of time steps

Re = round(l_cr * Uinf / nu) # Reynolds number

#%% intialization

u = cp.zeros((Nx, Ny, Nz)) # x-velocity

v = cp.zeros((Nx, Ny, Nz)) # y-velocity

w = cp.zeros((Nx, Ny, Nz)) # z-velocity

p = cp.zeros((Nx, Ny, Nz)) # pressure

X, Y, Z = cp.meshgrid(cp.linspace(0, L, Nx), cp.linspace(0, D, Ny), cp.linspace(0, W, Nz), indexing = 'ij') # spatial grid

#%% pre calculate for speed

P1 = 1 / (2 * h * dt)

P2 = 1 / (4 * h * h)

P3 = h**2

P4 = 1 / 6

P5 = (2 / Re) * dt / h**2

P6 = dt / h

P7 = 1 - (6 * P5)

P8 = 0.75 # under relaxation

P9 = 1 - P8

#%% create cube

cube_length = 1

cube_width = D

cube_depth = 1

center_x = cube_length / 2

center_y = cube_width / 2

center_z = cube_depth / 2

left_face = round((center_x - (cube_length / 2)) * Nx / L)

right_face = round((center_x + (cube_length / 2)) * Nx / L)

back_face = round((center_y - (cube_width / 2)) * Ny / D)

front_face = round((center_y + (cube_width / 2)) * Ny / D) - 1

bottom_face = round((center_z - (cube_depth / 2)) * Nz / W)

top_face = round((center_z + (cube_depth / 2)) * Nz / W)

#%% solve 3D Navier-Stokes equations

for nt in range(ns):

dudx = u[2:, 1:-1, 1:-1] - u[:-2, 1:-1, 1:-1]

dvdy = v[1:-1, 2:, 1:-1] - v[1:-1, :-2, 1:-1]

dwdz = w[1:-1, 1:-1, 2:] - w[1:-1, 1:-1, :-2]

pn = p.copy()

b = P1 * (dudx + dvdy + dwdz) - P2 * (dudx**2 + dvdy**2 + dwdz**2 + 2 * ((u[1:-1, 2:, 1:-1] - u[1:-1, :-2, 1:-1]) * (v[2:, 1:-1, 1:-1] - v[:-2, 1:-1, 1:-1]) + (u[1:-1, 1:-1, 2:] - u[1:-1, 1:-1, :-2]) * (w[2:, 1:-1, 1:-1] - w[:-2, 1:-1, 1:-1]) + (v[1:-1, 1:-1, 2:] - v[1:-1, 1:-1, :-2]) * (w[1:-1, 2:, 1:-1] - w[1:-1, :-2, 1:-1])))

p[1:-1, 1:-1, 1:-1] = P4 * (pn[2:, 1:-1, 1:-1] + pn[:-2, 1:-1, 1:-1] + pn[1:-1, 2:, 1:-1] + pn[1:-1, :-2, 1:-1] + pn[1:-1, 1:-1, 2:] + pn[1:-1, 1:-1, :-2] - P3 * b) # mass

p[0, :, :] = p[1, :, :] # dp/dx = 0 at x = 0

p[-1, :, :] = p[-2, :, :] # dp/dx = 0 at x = L

p[:, 0, :] = p[:, 1, :] # dp/dy = 0 at y = 0

p[:, -1, :] = p[:, -2, :] # dp/dy = 0 at y = D

p[:, :, 0] = p[:, :, 1] # dp/dz = 0 at z = 0

p[:, :, -1] = p[:, :, -2] # dp/dz = 0 at z = H

p[left_face:right_face, back_face:front_face, bottom_face:top_face] = 0

p[left_face, back_face:front_face, bottom_face:top_face] = p[left_face, back_face:front_face, bottom_face:top_face]

p[right_face, back_face:front_face, bottom_face:top_face] = p[right_face + 1, back_face:front_face, bottom_face:top_face]

p[left_face:right_face, front_face, bottom_face:top_face] = p[left_face:right_face, front_face, bottom_face:top_face]

p[left_face:right_face, back_face, bottom_face:top_face] = p[left_face:right_face, back_face, bottom_face:top_face]

p[left_face:right_face, back_face:front_face, bottom_face] = p[left_face:right_face, back_face:front_face, bottom_face]

p[left_face:right_face, back_face:front_face, top_face] = p[left_face:right_face, back_face:front_face, top_face + 1]

p = P8 * p + P9 * pn

un = u.copy()

vn = v.copy()

wn = w.copy()

u[1:-1, 1:-1, 1:-1] = un[1:-1, 1:-1, 1:-1] * P7 - P6 * (un[1:-1, 1:-1, 1:-1] * (un[2:, 1:-1, 1:-1] - un[:-2, 1:-1, 1:-1]) + vn[1:-1, 1:-1, 1:-1] * (un[1:-1, 2:, 1:-1] - un[1:-1, :-2, 1:-1]) + wn[1:-1, 1:-1, 1:-1] * (un[1:-1, 1:-1, 2:] - un[1:-1, 1:-1, :-2]) + p[2:, 1:-1, 1:-1] - p[:-2, 1:-1, 1:-1]) + P5 * (un[2:, 1:-1, 1:-1] + un[:-2, 1:-1, 1:-1] + un[1:-1, 2:, 1:-1] + un[1:-1, :-2, 1:-1] + un[1:-1, 1:-1, 2:] + un[1:-1, 1:-1, :-2]) # x momentum

u[0, :, :] = Uinf # u = 0 at x = 0

u[-1, :, :] = u[-2, :, :] # du/dx = 0 at # x = L

u[:, 0, :] = 0 # u = 0 at y = 0

u[:, -1, :] = 0 # u = 0 at y = D

u[:, :, 0] = 0 # u = 0 at z = 0

u[:, :, -1] = 0 # u = 0 at z = W

u[left_face:right_face, back_face:front_face, bottom_face:top_face] = 0

u[left_face, back_face:front_face, bottom_face:top_face] = 0

u[right_face, back_face:front_face, bottom_face:top_face] = 0

u[left_face:right_face, front_face, bottom_face:top_face] = 0

u[left_face:right_face, back_face, bottom_face:top_face] = 0

u[left_face:right_face, back_face:front_face, bottom_face] = 0

u[left_face:right_face, back_face:front_face, top_face] = 0

u = P8 * u + P9 * un

v[1:-1, 1:-1, 1:-1] = vn[1:-1, 1:-1, 1:-1] * P7 - P6 * (un[1:-1, 1:-1, 1:-1] * (vn[2:, 1:-1, 1:-1] - vn[:-2, 1:-1, 1:-1]) + vn[1:-1, 1:-1, 1:-1] * (vn[1:-1, 2:, 1:-1] - vn[1:-1, :-2, 1:-1]) + wn[1:-1, 1:-1, 1:-1] * (vn[1:-1, 1:-1, 2:] - vn[1:-1, 1:-1, :-2]) + p[1:-1, 2:, 1:-1] - p[1:-1, :-2, 1:-1]) + P5 * (vn[2:, 1:-1, 1:-1] + vn[:-2, 1:-1, 1:-1] + vn[1:-1, 2:, 1:-1] + vn[1:-1, :-2, 1:-1] + vn[1:-1, 1:-1, 2:] + vn[1:-1, 1:-1, :-2]) # y momentum

v[0, :, :] = 0 # v = 0 at x = 0

v[-1, :, :] = v[-2, :, :] # dv/dx = 0 at # x = L

v[:, 0, :] = 0 # v = 0 at y = 0

v[:, -1, :] = 0 # v = 0 at y = D

v[:, :, 0] = 0 # v = 0 at z = 0

v[:, :, -1] = 0 # v = 0 at z = W

v[left_face:right_face, back_face:front_face, bottom_face:top_face] = 0

v[left_face, back_face:front_face, bottom_face:top_face] = 0

v[right_face, back_face:front_face, bottom_face:top_face] = 0

v[left_face:right_face, front_face, bottom_face:top_face] = 0

v[left_face:right_face, back_face, bottom_face:top_face] = 0

v[left_face:right_face, back_face:front_face, bottom_face] = 0

v[left_face:right_face, back_face:front_face, top_face] = 0

v = P8 * v + P9 * vn

w[1:-1, 1:-1, 1:-1] = wn[1:-1, 1:-1, 1:-1] * P7 - P6 * (un[1:-1, 1:-1, 1:-1] * (wn[2:, 1:-1, 1:-1] - wn[:-2, 1:-1, 1:-1]) + vn[1:-1, 1:-1, 1:-1] * (wn[1:-1, 2:, 1:-1] - wn[1:-1, :-2, 1:-1]) + wn[1:-1, 1:-1, 1:-1] * (wn[1:-1, 1:-1, 2:] - wn[1:-1, 1:-1, :-2]) + p[1:-1, 1:-1, 2:] - p[1:-1, 1:-1, :-2]) + P5 * (wn[2:, 1:-1, 1:-1] + wn[:-2, 1:-1, 1:-1] + wn[1:-1, 2:, 1:-1] + wn[1:-1, :-2, 1:-1] + wn[1:-1, 1:-1, 2:] + wn[1:-1, 1:-1, :-2]) # z momentum

w[0, :, :] = 0 # w = 0 at x = 0

w[-1, :, :] = w[-2, :, :] # dw/dx = 0 at # x = L

w[:, 0, :] = 0 # w = 0 at y = 0

w[:, -1, :] = 0 # w = 0 at y = D

w[:, :, 0] = 0 # w = 0 at z = 0

w[:, :, -1] = 0 # w = 0 at z = W

w[left_face:right_face, back_face:front_face, bottom_face:top_face] = 0

w[left_face, back_face:front_face, bottom_face:top_face] = 0

w[right_face, back_face:front_face, bottom_face:top_face] = 0

w[left_face:right_face, front_face, bottom_face:top_face] = 0

w[left_face:right_face, back_face, bottom_face:top_face] = 0

w[left_face:right_face, back_face:front_face, bottom_face] = 0

w[left_face:right_face, back_face:front_face, top_face] = 0

w = P8 * w + P9 * wn

if nt % 1000 == 0:

print("% Complete", 100 * nt / ns)

#%% post process

u1 = u.copy() # u-velocity for plotting with box

v1 = v.copy() # v-velocity for plotting with box

w1 = w.copy() # v-velocity for plotting with box

p1 = p.copy() # pressure for plotting with box

u1[left_face:right_face, back_face:front_face, bottom_face:top_face] = cp.nan

v1[left_face:right_face, back_face:front_face, bottom_face:top_face] = cp.nan

w1[left_face:right_face, back_face:front_face, bottom_face:top_face] = cp.nan

p1[left_face:right_face, back_face:front_face, bottom_face:top_face] = cp.nan

fig = plt.figure(dpi = 500)

ax = fig.add_subplot(111, projection = '3d')

ax.contourf(X[:, Ny // 2, :].get(), u1[:, Ny // 2, :].get(), Z[:, Ny // 2, :].get(), zdir = 'y', offset = D / 2, levels = 128, cmap='jet', alpha = 0.5) # vertical plane

ax.set_xlim(0, L)

ax.set_ylim(0, D)

ax.set_zlim(0, W)

ax.set_xticks([0, L])

ax.set_yticks([0, D])

ax.set_zticks([0, W])

ax.tick_params(axis='x', labelsize = 4, pad = -2)

ax.tick_params(axis='y', labelsize = 4, pad = -2)

ax.tick_params(axis='z', labelsize = 4, pad = -2)

ax.set_xlabel('x [m]', fontsize = 4, labelpad = -15)

ax.set_ylabel('y [m]', fontsize = 4, labelpad = -15)

ax.set_zlabel('z [m]', fontsize = 4, labelpad = -15)

plt.gca().set_aspect('equal')

ax.view_init(elev = 22.5, azim = -45)

plt.show()

The resultant velocities and pressure field is shown in Fig. 1. The velocity iso-surfaces and streamlines along the plane of flow are shown with Fig. 2.

Fig. 1, Post-processing

Fig. 2, More post-processing

Thank you very much for reading! If you want to hire me as your next shining post-doc or collaborate in research, please reach out!

20th Step of the 12 Steps to Navier-Stokes 😑 (Heated Room)

In abundant spare time ⏳, yours truly has updated the code for 3D incompressible Navier–Stokes 🍃 equations using the finite-difference method with the ability to simulate species transport, for example heat or temperature. This post is a continuation of this post.

As before, this code 🖳 is fully vectorized 😲 with the only change being an addition of coupled energy equation. Steps 13 to 19 are available here. 13, 14, 15, 16, 17, 18, 19. Validation of the 2D code is available here and here. 🤓

NOTE: This method requires a GPU, if dear readers don't have a GPU then please stop being peasants... 🙉

If for some weird reason, you plan to use this code in your scholarly work, do cite this blog as:

Fahad Butt (2026). S-IBM (https://fluiddynamicscomputer.blogspot.com/2026/08/20th-step-of-12-steps-to-navier-stokes.html), Blogger. Retrieved Month Date, Year

Flow inside an empty room 📦 provides a complex 💢 flow 🌬 with very simple boundary conditions. This case has been widely used by researchers to validate the HVAC code. The case is solved at ~Re 4,000 without any turbulence models or wall functions. The room used in the simulation is 1 x 1 x 1 m. The inlet and outlet vents are 0.02 and 0.023 m wide. The floor of the room is at a higher temperature and remaining walls are at a lower temperature. The code is a simple 3D extension of this 2D code. The code to reproduce plots shown within Fig. 1 is available here ❗

#%% import libraries

import cupy as cp

import matplotlib.pyplot as plt

#%% define parameters

l_cr = 1 # characteristic length

h = 0.02 / 2 # grid spacing

dt = 0.001 # time step

L = 1 # domain length

D = 1 # domain depth

W = 1 # domain width

Nx = round(L / h) # grid points in x-axis

Ny = round(D / h) # grid points in y-axis

Nz = round(W / h) # grid points in z-axis

nu = 1 / 4000 # kinematic viscosity

Uinf = 1 # free stream velocity / inlet velocity / lid velocity

cfl = dt * Uinf / h # cfl number

travel = 5 # times the disturbance travels entire length of computational domain

TT = travel * L / Uinf # total time

ns = int(TT / dt) # number of time steps

Re = round(l_cr * Uinf / nu) # Reynolds number

Pr = 0.71465 # Prandtl number

alpha = 0.025969 # thermal conductivity

g = -9.81 # earth gravity

Tinf = 1 # free stream temperature

#%% intialization

u = cp.zeros((Nx, Ny, Nz)) # x-velocity

v = cp.zeros((Nx, Ny, Nz)) # y-velocity

w = cp.zeros((Nx, Ny, Nz)) # z-velocity

p = cp.zeros((Nx, Ny, Nz)) # pressure

T = (20/35) * cp.ones((Nx, Ny, Nz)) # temperature

X, Y, Z = cp.meshgrid(cp.linspace(0, L, Nx), cp.linspace(0, D, Ny), cp.linspace(0, W, Nz), indexing = 'ij') # spatial grid

#%% pre calculate for speed

P1 = 1 / (2 * h * dt)

P2 = 1 / (4 * h * h)

P3 = h**2

P4 = 1 / 6

P5 = (2 / Re) * dt / h**2

P6 = dt / h

P7 = 1 - (6 * P5)

P8 = 0.75 # under relaxation

P9 = 1 - P8

P10 = dt / (Re * Pr * h**2)

P11 = 1 - (6 * P10)

P12 = dt / (2 * h)

P13 = dt * alpha * g

P14 = round(0.023 * Ny / D)

P15 = round(0.98 * Ny / D)

#%% solve 3D Navier-Stokes equations

for nt in range(ns):

dudx = u[2:, 1:-1, 1:-1] - u[:-2, 1:-1, 1:-1]

dvdy = v[1:-1, 2:, 1:-1] - v[1:-1, :-2, 1:-1]

dwdz = w[1:-1, 1:-1, 2:] - w[1:-1, 1:-1, :-2]

pn = p.copy()

p[1:-1, 1:-1, 1:-1] = P4 * (pn[2:, 1:-1, 1:-1] + pn[:-2, 1:-1, 1:-1] + pn[1:-1, 2:, 1:-1] + pn[1:-1, :-2, 1:-1] + pn[1:-1, 1:-1, 2:] + pn[1:-1, 1:-1, :-2] - P3 * b) # mass

p[0, :, :] = p[1, :, :] # dp/dx = 0 at x = 0

p[-1, :, :] = p[-2, :, :] # dp/dx = 0 at x = L

p[:, 0, :] = p[:, 1, :] # dp/dy = 0 at y = 0

p[:, -1, :] = p[:, -2, :] # dp/dy = 0 at y = D

p[:, :, 0] = p[:, :, 1] # dp/dz = 0 at z = 0

p[:, :, -1] = p[:, :, -2] # dp/dz = 0 at z = H

p = P8 * p + P9 * pn

un = u.copy()

vn = v.copy()

wn = w.copy()

u[0, :, 0:P15] = 0 # u at x = 0

u[0, :, P15:] = Uinf # u at x = 0

u[-1, :, 0:P14] = u[-2, :, 0:P14] # u = 0 at # x = L

u[-1, :, P14:] = 0 # u = 0 at # x = L

u[:, 0, :] = 0 # u = 0 at y = 0

u[:, -1, :] = 0 # u = 0 at y = D

u[:, :, 0] = 0 # u = 0 at z = 0

u[:, :, -1] = 0 # u = Uinf at z = W

u = P8 * u + P9 * un

v[0, :, :] = 0 # v = 0 at x = 0

v[-1, :, 0:P14] = v[-2, :, 0:P14] # v = 0 at # x = L

v[-1, :, P14:] = 0 # v = 0 at # x = L

v[:, 0, :] = 0 # v = 0 at y = 0

v[:, -1, :] = 0 # v = 0 at y = D

v[:, :, 0] = 0 # v = 0 at z = 0

v[:, :, -1] = 0 # v = 0 at z = W

v = P8 * v + P9 * vn

w[0, :, :] = 0 # w = 0 at x = 0

w[-1, :, 0:P14] = w[-2, :, 0:P14] # w = 0 at # x = L

w[-1, :, P14:] = 0 # w = 0 at # x = L

w[:, 0, :] = 0 # w = 0 at y = 0

w[:, -1, :] = 0 # w = 0 at y = D

w[:, :, 0] = 0 # w = 0 at z = 0

w[:, :, -1] = 0 # w = 0 at z = W

w = P8 * w + P9 * wn

Tn = T.copy()

T[1:-1, 1:-1, 1:-1] = Tn[1:-1, 1:-1, 1:-1] * P11 - P12 * (un[1:-1, 1:-1, 1:-1] * (Tn[2:, 1:-1, 1:-1] - Tn[:-2, 1:-1, 1:-1]) + vn[1:-1, 1:-1, 1:-1] * (Tn[1:-1, 2:, 1:-1] - Tn[1:-1, :-2, 1:-1]) + wn[1:-1, 1:-1, 1:-1] * (Tn[1:-1, 1:-1, 2:] - Tn[1:-1, 1:-1, :-2])) + P10 * (Tn[2:, 1:-1, 1:-1] + Tn[:-2, 1:-1, 1:-1] + Tn[1:-1, 2:, 1:-1] + Tn[1:-1, :-2, 1:-1] + Tn[1:-1, 1:-1, 2:] + Tn[1:-1, 1:-1, :-2]) # energy

T[0, :, :] = 0.43 # x = 0

T[-1, :, :] = 0.43 # x = L

T[:, 0, :] = 0.43 # y = 0

T[:, -1, :] = 0.43 # y = D

T[:, :, 0] = Tinf # z = 0

T[:, :, -1] = 0.43 # z = W

T = P8 * T + P9 * Tn

if nt % 1000 == 0:

print("% Complete", 100 * nt / ns)

#%% post process

fig = plt.figure(dpi = 500)

ax = fig.add_subplot(111, projection = '3d')

ax.contourf(X[:, Ny // 2, :].get(), u[:, Ny // 2, :].get(), Z[:, Ny // 2, :].get(), zdir = 'y', offset = D / 2, levels = 128, cmap='jet', alpha = 0.5) # vertical plane

ax.set_xlim(0, L)

ax.set_ylim(0, D)

ax.set_zlim(0, W)

ax.set_xticks([0, L])

ax.set_yticks([0, D])

ax.set_zticks([0, W])

ax.tick_params(axis='x', pad=-2)

ax.tick_params(axis='y', pad=-2)

ax.tick_params(axis='z', pad=-2)

ax.set_xlabel('x [m]', labelpad = -15)

ax.set_ylabel('y [m]', labelpad = -15)

ax.set_zlabel('z [m]', labelpad = -15)

plt.gca().set_aspect('equal')

ax.view_init(elev = 22.5, azim = -45)

plt.show()

The results from post processing are shown in Fig. 1. Within Fig. 1, the u, v and w components of velocities and room temperature are shown along the plane of flow.

Fig. 1, post processing

If you want to hire me as your next shining post-doc or collaborate in research, please reach out! Thank you very much for reading!

Monday, 10 August 2026

19th Step of the 12 Steps to Navier-Stokes 😑 (3D-Lid Driven Cavity)

One fine morning (in abundant spare time ⏳, of course), yours truly decided to code the 3D incompressible Navier–Stokes 🍃 equations using the finite-difference method. This post has the results of this adventure 🏞️ (so-far). As is customary with all my CFD work using commercial and home-made CFD codes, this too is an unofficial continuation of the series by Dr. Lorena Barba.

The code 🖳 shared in this post is fully vectorized 😲. Steps 13 to 18 are available here. 13, 14, 15, 16, 17, 18. Validation of the 2D code is available here and here. 🤓

NOTE: This method requires a GPU, if dear readers don't have a GPU then please stop being peasants... 🙉

If for some reason, you plan to use these codes in your scholarly work, do cite this blog as:

Fahad Butt (2026). S-IBM (https://fluiddynamicscomputer.blogspot.com/2026/08/19th-step-of-12-steps-to-navier-stokes.html), Blogger. Retrieved Month Date, Year

Lid-Driven Cavity 🕳 provides a complex 💢 flow 🌬 with very simple boundary conditions. Literally, everyone else uses this case to validate the code they write. The lid-driven cavity case is solved at ~Re 1,000 without any turbulence models or wall functions. The cavity used in the simulation is 1 x 1 x 1 m. This code is a simple 3D extension of this code. Well, the code is double in length as the 3D version requires under-relaxation and has one more momentum equation. Still, it is less than 100 lines ❗ The code is available here.

#%% import libraries

import cupy as cp

import matplotlib.pyplot as plt

#%% define parameters

l_cr = 1 # characteristic length

h = l_cr / 100 # grid spacing

dt = 0.001 # time step

L = 1 # domain length

D = 1 # domain depth

W = 1 # domain width

Nx = round(L / h) # grid points in x-axis

Ny = round(D / h) # grid points in y-axis

Nz = round(W / h) # grid points in z-axis

nu = 1 / 1000 # kinematic viscosity

Uinf = 1 # free stream velocity / inlet velocity / lid velocity

cfl = dt * Uinf / h # cfl number

travel = 10 # times the disturbance travels entire length of computational domain

TT = travel * L / Uinf # total time

ns = int(TT / dt) # number of time steps

Re = round(l_cr * Uinf / nu) # Reynolds number

#%% intialization

u = cp.zeros((Nx, Ny, Nz)) # x-velocity

v = cp.zeros((Nx, Ny, Nz)) # y-velocity

w = cp.zeros((Nx, Ny, Nz)) # z-velocity

p = cp.zeros((Nx, Ny, Nz)) # pressure

X, Y, Z = cp.meshgrid(cp.linspace(0, L, Nx), cp.linspace(0, D, Ny), cp.linspace(0, W, Nz), indexing = 'ij') # spatial grid

#%% pre calculate for speed

P1 = 1 / (2 * h * dt)

P2 = 1 / (4 * h * h)

P3 = h**2

P4 = 1 / 6

P5 = (2 / Re) * dt / h**2

P6 = dt / h

P7 = 1 - (6 * P5)

P8 = 0.75 # under relaxation

P9 = 1 - P8

#%% solve 3D Navier-Stokes equations

for nt in range(ns):

dudx = u[2:, 1:-1, 1:-1] - u[:-2, 1:-1, 1:-1]

dvdy = v[1:-1, 2:, 1:-1] - v[1:-1, :-2, 1:-1]

dwdz = w[1:-1, 1:-1, 2:] - w[1:-1, 1:-1, :-2]

pn = p.copy()

p[1:-1, 1:-1, 1:-1] = P4 * (pn[2:, 1:-1, 1:-1] + pn[:-2, 1:-1, 1:-1] + pn[1:-1, 2:, 1:-1] + pn[1:-1, :-2, 1:-1] + pn[1:-1, 1:-1, 2:] + pn[1:-1, 1:-1, :-2] - P3 * b) # mass

p[0, :, :] = p[1, :, :] # dp/dx = 0 at x = 0

p[-1, :, :] = p[-2, :, :] # dp/dx = 0 at x = L

p[:, 0, :] = p[:, 1, :] # dp/dy = 0 at y = 0

p[:, -1, :] = p[:, -2, :] # dp/dy = 0 at y = D

p[:, :, 0] = p[:, :, 1] # dp/dz = 0 at z = 0

p[:, :, -1] = p[:, :, -2] # dp/dz = 0 at z = H

p = P8 * p + P9 * pn

un = u.copy()

vn = v.copy()

wn = w.copy()

u[0, :, :] = 0 # u = 0 at x = 0

u[-1, :, :] = 0 # u = 0 at # x = L

u[:, 0, :] = 0 # u = 0 at y = 0

u[:, -1, :] = 0 # u = 0 at y = D

u[:, :, 0] = 0 # u = 0 at z = 0

u[:, :, -1] = Uinf # u = Uinf at z = W

u = P8 * u + P9 * un

v[0, :, :] = 0 # v = 0 at x = 0

v[-1, :, :] = 0 # v = 0 at # x = L

v[:, 0, :] = 0 # v = 0 at y = 0

v[:, -1, :] = 0 # v = 0 at y = D

v[:, :, 0] = 0 # v = 0 at z = 0

v[:, :, -1] = 0 # v = 0 at z = W

v = P8 * v + P9 * vn

w[0, :, :] = 0 # w = 0 at x = 0

w[-1, :, :] = 0 # w = 0 at # x = L

w[:, 0, :] = 0 # w = 0 at y = 0

w[:, -1, :] = 0 # w = 0 at y = D

w[:, :, 0] = 0 # w = 0 at z = 0

w[:, :, -1] = 0 # w = 0 at z = W

w = P8 * w + P9 * wn

if nt % 1000 == 0:

print("% Complete", 100 * nt / ns)

#%% post process

fig = plt.figure(dpi = 500)

ax = fig.add_subplot(111, projection = '3d')

ax.contourf(X[:, Ny // 2, :].get(), u[:, Ny // 2, :].get(), Z[:, Ny // 2, :].get(), zdir = 'y', offset = D / 2, levels = 128, cmap='jet', alpha = 0.5) # vertical plane

ax.set_xlim(0, L)

ax.set_ylim(0, D)

ax.set_zlim(0, W)

ax.set_xticks([0, L])

ax.set_yticks([0, D])

ax.set_zticks([0, W])

ax.tick_params(axis='x', pad = -2)

ax.tick_params(axis='y', pad = -2)

ax.tick_params(axis='z', pad = -2)

ax.set_xlabel('x [m]', labelpad = -15)

ax.set_ylabel('y [m]', labelpad = -15)

ax.set_zlabel('z [m]', labelpad = -15)

plt.gca().set_aspect('equal')

ax.view_init(elev = 22.5, azim = -45)

plt.show()

The results from post processing are shown in Fig. 1. Within Fig. 1, the u, v and w components of velocities are shown along the plane of flow. The resulting pressure field and the velocity streamlines are shown within Fig. 2.

Fig. 1, Velocity components

Fig. 2, The pressure field and streamlines

If you want to hire me as your next shining post-doc or collaborate in research, please reach out! Thank you very much for reading!

Monday, 17 November 2025

A Simple Poisson's Equation for Pressure

In abundant spare time 🕰️, yours truly has removed ❌ the non-linear 〰️ terms from the Pressure Poisson Equation (PPE) which is derived 🎡 by summing the divergence of momentum equations and then applying conservation of mass ⚖️. The non-linear terms create a problem in convergence. Therefore, inspired by the style of work of the "Skipper"🐧, yours truly removed the problem causing non-linear terms 😀. The derived PPE is mentioned by equation 1. The PPE used in the code yours truly has developed is mention in equation 2. Within equations 1 and 2, the u and v are components of velocity along x and y-axis. The pressure is represented by p and while, t represents the time.

∂²p/∂x² + ∂²p/∂y² = 1/∆t * (∂u/∂x + ∂v/∂y - (∂u/∂x)² - (∂v/∂y)² - 2*∂v/∂y*∂u/∂x) [1]

∂²p/∂x² + ∂²p/∂y² = 1/(2 * ∆t) * (∂u/∂x + ∂v/∂y) [2]

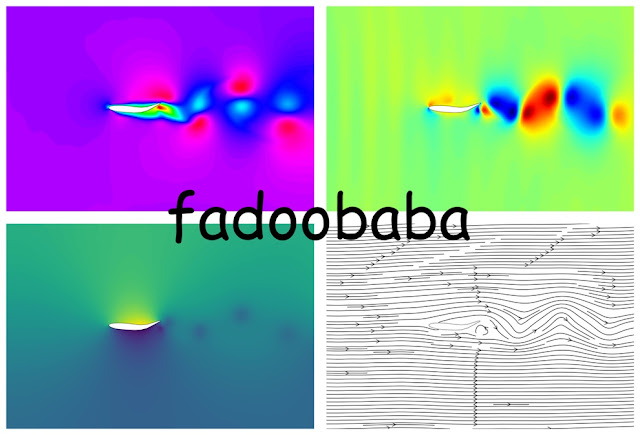
For the same grid and for solving the same problem, the time-step supported by equation 2 is 40x more as compared to equation 1. Therefore, the resultant compute per watt is 40x less for equation 2 as compared to equation 1 🤯. The code for equation 1 is shown first, followed by the code for equation 2. The results are compared via streamlines and pressure contours, with in Fig. 1. The benchmark case solved is of the lid-driven cavity which offer simple implementation and very complex flow physics. For validation of the code, refer to here, here and here.

Permission is hereby granted, free of charge, to any person obtaining a copy of this software and associated documentation files (the “Software”), to deal in the Software without restriction, including without limitation the rights to use, copy, modify, merge, publish, distribute, sublicense, and/or sell copies of the Software, and to permit persons to whom the Software is furnished to do so, subject to the following conditions:

The above copyright notice and this permission notice shall be included in all copies or substantial portions of the Software.

THE SOFTWARE IS PROVIDED “AS IS”, WITHOUT WARRANTY OF ANY KIND, EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY, FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE SOFTWARE.

If you are mad 👨‍🔬 enough to use this code in your scholarly 👨‍🏫 work, then please remember to cite: Fahad Butt (2025). S-PPE (https://fluiddynamicscomputer.blogspot.com/2025/11/a-simple-poissons-equation-for-pressure.html), Blogger. Retrieved Month Date, Year

MANDATORY NOTE: This method requires a GPU, if dear readers don't have a GPU then please stop being peasants... 🙉

Code 01

#%% import libraries

import cupy as cp

import matplotlib.pyplot as plt

#%% define parameters

l_cr = 1 # characteristic length

h = l_cr / 100 # grid spacing

dt = 0.00005 # time step

L = 1 # domain length

D = 1 # domain depth

Nx = round(L / h) + 1 # grid points in x-axis

Ny = round(D / h) + 1 # grid points in y-axis

nu = 1 / 400 # kinematic viscosity

Uinf = 1 # free stream velocity / inlet velocity / lid velocity

cfl = dt * Uinf / h # cfl number

travel = 10 # times the disturbance travels entire length of computational domain

TT = travel * L / Uinf # total time

ns = int(TT / dt) # number of time steps

Re = round(l_cr * Uinf / nu) # Osborne Reynolds and his number :)

#%% intialization (t = 0)

u = cp.zeros((Nx, Ny)) # x-velocity

v = cp.zeros((Nx, Ny)) # y-velocity

p = cp.zeros((Nx, Ny)) # pressure

X, Y = cp.meshgrid(cp.linspace(0, L, Nx), cp.linspace(0, D, Ny), indexing = 'ij') # spatial grid

#%% pre calculate for speed

P1 = h / (8 * dt)

P2 = (2 / Re) * dt / h**2

P3 = dt / h

P4 = 1 - (4 * P2)

#%% solve 2D incompressible Navier-Stokes equations

for _ in range(ns):

pn = p.copy()

p[1:-1, 1:-1] = 0.25 * (pn[2:, 1:-1] + pn[:-2, 1:-1] + pn[1:-1, 2:] + pn[1:-1, :-2]) - P1 * ((u[2:, 1:-1] - u[:-2, 1:-1] + v[1:-1, 2:] - v[1:-1, :-2]) - (u[2:, 1:-1] - u[:-2, 1:-1])**2 - (v[1:-1, 2:] - v[1:-1, :-2])**2 - (2 * (u[2:, 1:-1] - u[:-2, 1:-1]) * (v[1:-1, 2:] - v[1:-1, :-2]))) # pressure

p[0, :] = p[1, :] # dp/dx = 0 at x = 0

p[-1, :] = p[-2, :] # dp/dx = 0 at x = L

p[:, 0] = p[:, 1] # dp/dy = 0 at y = 0

p[:, -1] = p[:, -2] # dp/dy = 0 at y = D

un = u.copy()

vn = v.copy()

u[1:-1, 1:-1] = un[1:-1, 1:-1] * P4 - P3 * (un[1:-1, 1:-1] * (un[2:, 1:-1] - un[:-2, 1:-1]) + vn[1:-1, 1:-1] * (un[1:-1, 2:] - un[1:-1, :-2]) + p[2:, 1:-1] - p[:-2, 1:-1]) + P2 * (un[2:, 1:-1] + un[:-2, 1:-1] + un[1:-1, 2:] + un[1:-1, :-2]) # x momentum

u[0, :] = 0 # u = Uinf at x = 0

u[-1, :] = 0 # u = 0 at x = L

u[:, 0] = 0 # u = 0 at y = 0

u[:, -1] = Uinf # u = Uinf at y = D

v[1:-1, 1:-1] = vn[1:-1, 1:-1] * P4 - P3 * (un[1:-1, 1:-1] * (vn[2:, 1:-1] - vn[:-2, 1:-1]) + vn[1:-1, 1:-1] * (vn[1:-1, 2:] - vn[1:-1, :-2]) + p[1:-1, 2:] - p[1:-1, :-2]) + P2 * (vn[2:, 1:-1] + vn[:-2, 1:-1] + vn[1:-1, 2:] + vn[1:-1, :-2]) # y momentum

v[0, :] = 0 # v = 0 at x = 0

v[-1, :] = 0 # v = 0 at x = L

v[:, 0] = 0 # v = 0 at y = 0

v[:, -1] = 0 # v = 0 at y = D

Code 2

#%% import libraries

import cupy as cp

import matplotlib.pyplot as plt

#%% define parameters

l_cr = 1 # characteristic length

h = l_cr / 100 # grid spacing

dt = 0.002 # time step

L = 1 # domain length

D = 1 # domain depth

Nx = round(L / h) + 1 # grid points in x-axis

Ny = round(D / h) + 1 # grid points in y-axis

nu = 1 / 400 # kinematic viscosity

Uinf = 1 # free stream velocity / inlet velocity / lid velocity

cfl = dt * Uinf / h # cfl number

travel = 10 # times the disturbance travels entire length of computational domain

TT = travel * L / Uinf # total time

ns = int(TT / dt) # number of time steps

Re = round(l_cr * Uinf / nu) # Osborne Reynolds and his number :)

#%% intialization (t = 0)

u = cp.zeros((Nx, Ny)) # x-velocity

v = cp.zeros((Nx, Ny)) # y-velocity

p = cp.zeros((Nx, Ny)) # pressure

X, Y = cp.meshgrid(cp.linspace(0, L, Nx), cp.linspace(0, D, Ny), indexing = 'ij') # spatial grid

#%% pre calculate for speed

P1 = h / (16 * dt)

P2 = (2 / Re) * dt / h**2

P3 = dt / h

P4 = 1 - (4 * P2)

#%% solve 2D incompressible Navier-Stokes equations

for _ in range(ns):

pn = p.copy()

p[1:-1, 1:-1] = 0.25 * (pn[2:, 1:-1] + pn[:-2, 1:-1] + pn[1:-1, 2:] + pn[1:-1, :-2]) - P1 * (u[2:, 1:-1] - u[:-2, 1:-1] + v[1:-1, 2:] - v[1:-1, :-2]) # mass

p[0, :] = p[1, :] # dp/dx = 0 at x = 0

p[-1, :] = p[-2, :] # dp/dx = 0 at x = L

p[:, 0] = p[:, 1] # dp/dy = 0 at y = 0

p[:, -1] = p[:, -2] # dp/dy = 0 at y = D

un = u.copy()

vn = v.copy()

u[0, :] = 0 # u = Uinf at x = 0

u[-1, :] = 0 # u = 0 at x = L

u[:, 0] = 0 # u = 0 at y = 0

u[:, -1] = Uinf # u = Uinf at y = D

v[0, :] = 0 # v = 0 at x = 0

v[-1, :] = 0 # v = 0 at x = L

v[:, 0] = 0 # v = 0 at y = 0

v[:, -1] = 0 # v = 0 at y = D

Fig. 1, pressure range for both cases is 0 (blue) till 1 (red).

If you want to hire me as your next shining post-doc or collaborate in research, please reach out! Thank you for reading!

Fluid Dynamics using the Computer

My Blogger Profile

Wednesday, 12 August 2026

21st Step of the 12 steps to Navier-Stokes 😑 (3D Backwards Facing Step)

20th Step of the 12 Steps to Navier-Stokes 😑 (Heated Room)

Monday, 10 August 2026

19th Step of the 12 Steps to Navier-Stokes 😑 (3D-Lid Driven Cavity)

Monday, 17 November 2025

A Simple Poisson's Equation for Pressure

Code 01

Code 2