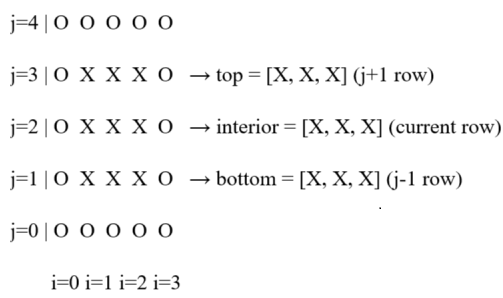This is probably the final step in the series. Unless, one fine morning yours truly randomly decides to write about moving and morphing airfoils 😑 i.e. a true virtual wind tunnel 🤓.
This post is about flow around shape changing 🪱 obstacles i.e. morphing wings. The development of these codes shared here, including the one mentioned in this post, started in the year 2020 and continued till the fall of 2023. All this effort was to create a digital CV so that yours truly can get himself accepted in to a funded PhD program. That happened in fall 2023 😌.
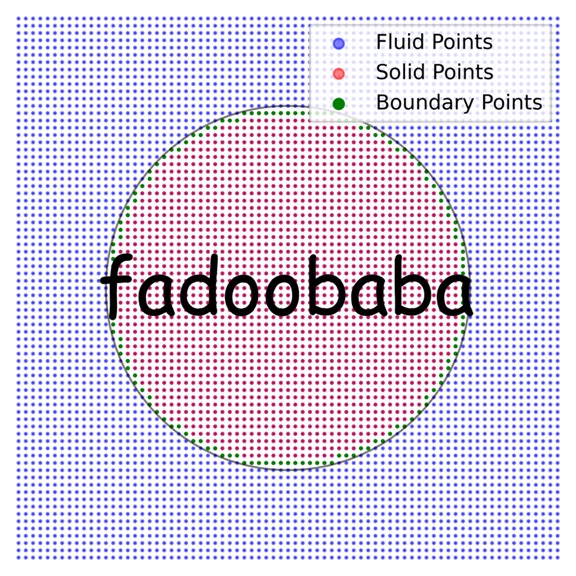
The frequency of oscillations, the equations for amplitude and lateral oscillations 〰️ are all taken from the published literature about swimming fish 🐟. As a starting point, the NACA 0012 airfoil is used. A polygon is then created. Each grid index is then tested for presence inside or outside the polygon. An index is marked as the boundary of the polygon if one index has anyone neighboring index outside the polygon. The neighboring boundary indices are used to apply Neumann boundary conditions for pressure. The boundary indices are used to apply no-slip Dirichlet boundary conditions on the polygon boundary. More details can be read here.
Because the camber of airfoil changes at each time-step, approximately 400 points are required on the airfoil boundary to properly capture the time-varying camber of the airfoil i.e. the fish 🐋. The output from the code is shown in Fig. 1. Within Fig. 1, top row has u and v components of velocity. Meanwhile, the bottom row shows the pressure and streamlines. The animation is shown in Fig. 2.
If you plan to use these codes in your scholarly work, do cite this blog as:
Fig. 2, Animation
#Copyright <2025> <FAHAD BUTT>
#Permission is hereby granted, free of charge, to any person obtaining a copy of this software and associated documentation files (the “Software”), to deal in the Software without restriction, including without limitation the rights to use, copy, modify, merge, publish, distribute, sublicense, and/or sell copies of the Software, and to permit persons to whom the Software is furnished to do so, subject to the following conditions:
#The above copyright notice and this permission notice shall be included in all copies or substantial portions of the Software.
#THE SOFTWARE IS PROVIDED “AS IS”, WITHOUT WARRANTY OF ANY KIND, EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY, FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE SOFTWARE.
#%% import libraries
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.path import Path
#%% define parameters
l_cr = 1 # characteristic length
h = l_cr / 400 # grid spacing
dt = 0.00001 # time step
L = 8 # domain length
D = 4 # domain depth
Nx = round(L / h) + 1 # grid points in x-axis
Ny = round(D / h) + 1 # grid points in y-axis
nu = 1 / 500 # kinematic viscosity
Uinf = 1 # free stream velocity / inlet velocity / lid velocity
cfl = dt * Uinf / h # cfl number
Re = round(l_cr * Uinf / nu) # Reynolds number
#%% intialization
u = Uinf * np.ones((Nx, Ny)) # x-velocity
v = np.zeros((Nx, Ny)) # y-velocity
p = np.zeros((Nx, Ny)) # pressure
X, Y = np.meshgrid(np.linspace(0, L, Nx), np.linspace(0, D, Ny)) # spatial grid
#%% pre calculate for speed
P1 = h / (16 * dt)
P2 = (2 / Re) * dt / h**2
P3 = dt / h
P4 = 1 - (4 * P2)
#%% motion parameters
freq = 0.8 # frequency of oscillation (from litrature)
factor = 2 * np.pi * freq # 2 * pi * f
TP = 1 / freq # time period
ns = int(6 * TP / dt) # number of time steps
t = 0.12 # airfoil thickness
c = 1 # airfoil chord length
num_points = 150 # points along chord
alpha = np.linspace(0, np.pi, num_points) # angle values
x_airfoil = 0.5 * (1 - np.cos(alpha)) * c # cosine spacing on x coordinates
x_frac = x_airfoil / c # normalized airfoil x coordinates
a0 = 0.02 # amplitude co efficient a0 (from litrature)
a1 = 0.01 # amplitude co efficient a1
a2 = 0.1 # amplitude co efficient a2
a_x = a0 + a1 * x_frac + a2 * x_frac**2 # amplitude of oscillation (from litrature)
yt = 5 * t * (0.2969 * np.sqrt(x_airfoil) - 0.1260 * x_airfoil - 0.3516 * x_airfoil**2 + 0.2843 * x_airfoil**3 - 0.1036 * x_airfoil**4) # airfoil co ordinates
foil_center_x = L / 3 # foil center x
foil_center_y = D / 2 # foil center y
x1 = foil_center_x + np.concatenate([x_airfoil, x_airfoil[::-1]]) # foil x
#%% solve 2D Navier-Stokes equations
for nt in range(ns):
y_oscillation = a_x * np.cos(2 * np.pi * x_frac - factor * nt * dt) # lateral oscillation (from litrature)
y_top = y_oscillation + yt # airfoil top
y_bottom = y_oscillation - yt # airfoil bottom
y1 = foil_center_y + np.concatenate([y_top, y_bottom[::-1]]) # foil y
foil_path = Path(np.column_stack((x1, y1))) # foil region (polygon)
points = np.vstack((X.ravel(), Y.ravel())).T # check if inside region
custom_curve = foil_path.contains_points(points).reshape(X.shape) # test all grid points for inclusion in airfoil, contains_points returns True for each point inside the airfoil (polygon)
curve = custom_curve.T # transpose to match grid orientation
boundary_mask = np.zeros_like(curve, dtype = bool) # create boolean mask
interior = curve[1:-1, 1:-1] # interior of foil
right = curve[2:, 1:-1] # boolean arrays indicating if neighbors of each interior point are inside airfoil (polygon)
left = curve[:-2, 1:-1]
top = curve[1:-1, 2:]
bottom = curve[1:-1, :-2]
boundary = interior & ~(right & left & top & bottom) # mark if point is inside foil and at least one neighbor is outside foil (mark interface between solid and fluid)
boundary_mask[1:-1, 1:-1] = boundary # fill the empty boundary
custom_curve_boundary = boundary_mask.T # transpose back
boundary_indices = np.where(custom_curve_boundary.T) # mark boundary indices
right_neighbors = (boundary_indices[0] + 1, boundary_indices[1]) # right index (neighboring grid points in each direction)
left_neighbors = (boundary_indices[0] - 1, boundary_indices[1]) # left index
top_neighbors = (boundary_indices[0], boundary_indices[1] + 1) # top index
bottom_neighbors = (boundary_indices[0], boundary_indices[1] - 1) # bottom index
# identify valid neighbor indices, ensure the neighbor is not inside airfoil (polygon) i.e. is inside fluid)
valid_right = (boundary_indices[0] + 1 < X.shape[0]) & (~curve[right_neighbors])
valid_left = (boundary_indices[0] - 1 >= 0) & (~curve[left_neighbors])
valid_top = (boundary_indices[1] + 1 < X.shape[1]) & (~curve[top_neighbors])
valid_bottom = (boundary_indices[1] - 1 >= 0) & (~curve[bottom_neighbors])
pn = p.copy()
p[1:-1, 1:-1] = 0.25 * (pn[2:, 1:-1] + pn[:-2, 1:-1] + pn[1:-1, 2:] + pn[1:-1, :-2]) - P1 * (u[2:, 1:-1] - u[:-2, 1:-1] + v[1:-1, 2:] - v[1:-1, :-2]) # pressure
p[0, :] = p[1, :] # dp/dx = 0 at x = 0
p[-1, :] = p[-2, :] # dp/dx = 0 at x = L
p[:, 0] = p[:, 1] # dp/dy = 0 at y = 0
p[:, -1] = p[:, -2] # dp/dy = 0 at y = D
p[curve] = 0 # p = 0 inside shape
p[boundary_indices] = np.where(valid_right, p[right_neighbors], p[boundary_indices]) # right neighbor is fluid
p[boundary_indices] = np.where(valid_left, p[left_neighbors], p[boundary_indices]) # left neighbor is fluid
p[boundary_indices] = np.where(valid_top, p[top_neighbors], p[boundary_indices]) # top neighbor is fluid
p[boundary_indices] = np.where(valid_bottom, p[bottom_neighbors], p[boundary_indices]) # bottom neighbor is fluid
un = u.copy()
vn = v.copy()
u[1:-1, 1:-1] = un[1:-1, 1:-1] * P4 - P3 * (un[1:-1, 1:-1] * (un[2:, 1:-1] - un[:-2, 1:-1]) + vn[1:-1, 1:-1] * (un[1:-1, 2:] - un[1:-1, :-2]) + p[2:, 1:-1] - p[:-2, 1:-1]) + P2 * (un[2:, 1:-1] + un[:-2, 1:-1] + un[1:-1, 2:] + un[1:-1, :-2]) # x momentum
u[0, :] = Uinf # u = Uinf at x = 0
u[-1, :] = u[-2, :] # du/dx = 0 at x = L
u[:, 0] = Uinf # u = Uinf at y = 0
u[:, -1] = Uinf # u = Uinf at y = D
u[curve] = 0 # u = 0 inside shape
u[custom_curve_boundary.T] = 0 # no slip
v[1:-1, 1:-1] = vn[1:-1, 1:-1] * P4 - P3 * (un[1:-1, 1:-1] * (vn[2:, 1:-1] - vn[:-2, 1:-1]) + vn[1:-1, 1:-1] * (vn[1:-1, 2:] - vn[1:-1, :-2]) + p[1:-1, 2:] - p[1:-1, :-2]) + P2 * (vn[2:, 1:-1] + vn[:-2, 1:-1] + vn[1:-1, 2:] + vn[1:-1, :-2]) # y momentum
v[0, :] = 0 # v = 0 at x = 0
v[-1, :] = v[-2, :] # dv/dx = 0 at x = L
v[:, 0] = 0 # v = 0 at y = 0
v[:, -1] = 0 # v = 0 at y = D
v[curve] = 0 # u = 0 inside shape
v[custom_curve_boundary.T] = 0 # no slip
boundary_x = X[boundary_indices[1], boundary_indices[0]] # get actual x-coordinate values of all boundary points
x_frac_boundary = (boundary_x - foil_center_x) / c # normalized streamwise position along the airfoil for each boundary point
vinf_foil_boundary = (a0 + a1 * x_frac_boundary + a2 * x_frac_boundary**2) * factor * np.sin(2 * np.pi * x_frac_boundary - factor * nt * dt) # vertical velocity at boundaries
v[top_neighbors] = vinf_foil_boundary # above the boundary
v[bottom_neighbors] = vinf_foil_boundary # below the boundary
v[right_neighbors] = vinf_foil_boundary # right of boundary
v[left_neighbors] = vinf_foil_boundary # left of boundary
#%% post process
u1 = u.copy() # u-velocity for plotting with foil
v1 = v.copy() # v-velocity for plotting with foil
p1 = p.copy() # pressure for plotting with foil
u1[custom_curve.T] = np.nan # shape geometry for plotting
v1[custom_curve.T] = np.nan
p1[custom_curve.T] = np.nan
velocity_magnitude1 = np.sqrt(u1**2 + v1**2) # velocity magnitude with shape
# visualize velocity vectors and pressure contours
plt.figure(dpi = 500)
plt.contourf(X, Y, u1.T, 128, cmap = 'jet')
plt.plot(x1, y1, color='black', alpha = 1, linewidth = 1)
plt.colorbar()
plt.gca().set_aspect('equal', adjustable='box')
plt.xticks([0, L])
plt.yticks([0, D])
plt.xlabel('x [m]')
plt.ylabel('y [m]')
plt.axis('off')
plt.show()
plt.figure(dpi = 500)
plt.contourf(X, Y, v1.T, 128, cmap = 'jet')
plt.plot(x1, y1, color='black', alpha = 1, linewidth = 1)
plt.colorbar()
plt.gca().set_aspect('equal', adjustable='box')
plt.xticks([0, L])
plt.yticks([0, D])
plt.xlabel('x [m]')
plt.ylabel('y [m]')
plt.axis('off')
plt.show()
plt.figure(dpi = 500)
plt.contourf(X, Y, p1.T, 128, cmap = 'jet')
plt.plot(x1, y1, color='black', alpha = 1, linewidth = 1)
plt.colorbar()
plt.gca().set_aspect('equal', adjustable='box')
plt.xticks([0, L])
plt.yticks([0, D])
plt.xlabel('x [m]')
plt.ylabel('y [m]')
plt.axis('off')
plt.show()
plt.figure(dpi = 500)
plt.streamplot(X, Y, u1.T, v1.T, color = 'black', cmap = 'jet', density = 2, linewidth = 0.5, arrowstyle='->', arrowsize = 1) # plot streamlines
plt.plot(x1, y1, color='black', alpha = 1, linewidth = 1)
plt.gca().set_aspect('equal', adjustable = 'box')
plt.xlim([0, L])
plt.ylim([0, D])
plt.axis('off')
plt.show()
Thank you for reading! If you want to hire me as a post-doc researcher in the fields of thermo-fluids and / or fracture mechanics, do reach out!